DEFİNE--DEFİNECİLİK-DEFİNE İŞARETLERİ-DEFİNE İŞARET ÇÖZÜMLERİ-DEFİNE HARİTALARI-HAZİNELER-DEDEKTÖR-DEFİNE ARAMA ÇUBUKLARI YAPIMI-GPR-ALTIN-GÜMÜŞ-ELMAS-TILSIM-GİZEMLER-GÖMÜ-SİKKE-CİN-EŞKİYA BELGELERİ-MEZAR TÜRLERİ-HÖYÜK-TÜMÜLÜS-KAYA MEZARI-MEDENİYETLER-EFSANELER-DESTANLAR-BÜYÜ VE BÜYÜCÜLÜK-KEHANET-ÜNLÜ EŞKİYALAR-ARKEOLOJİ-TARİHTE PARA-TAKILAR-DOĞAL TAŞLAR-DARPHANE-MÜZELER HAKKINDA BİLGİLER-DİNİMİZ İSLAM-DEFİNE HABERLERİ-TÜRK DÜNYASI-MİTOLOJİ-HEYKEL-ANTİK MISIR-ANTİKA NÜMİZMATİK-TÜRKİYEDE ARKEOLOJİ-ANTİK BÖLGELER-ANTİK KENTLER-TARİH VE TARİHİN YARARLANDIĞI BİLİMLER-HORASAN-ÖLÇÜ VE AĞIRLIK BİRİMLERİ-ÖLÇME ALETLERİ-TARİHİ TİCARET YOLLARI-EBCED HESABI-İŞARET ÇÖZÜMLERİ-DEFİNE ARAMA YOLLARI-GİZEMLİ DEFİNERİ BULMA-HORASAN ÇÖZME-KAYA MEZARLARI- MEZAR-ROMA SİKKE-BİZANS SİKKE-GREEK SİKKE-TARİHİ ANTİK SİKKE VE PARALAR-ARKEOLOJİ VE DEFİNECİLİK ÜZERİNE HER TÜRLÜ BİLGİ DEFİNE SIRLARINDA...http://www.definesirlari.com
İlkçağ insanı (ilkel insan, mağara insanı), rakam ve sayıları kullanmak ihtiyacını duymuştur. Bu devir insanları, ihtiyaçlarını kaydedip saklamasını da biliyordu. Avladıkları hayvanların veya sürüsündeki koyunların sayılarını belirtmek için, yaşadıkları mağara duvarlarına çizikler çizmişler, bir ağaç dalına çentikler yapmışlardır. Bazen de, ipe düğüm atmışlar, veya çakıl taşlarını kullanmışlardır .
Bu devrin, 13-15 yaşındaki insanı, koyun ve geyik gibi varlıkları, ok gibi eşyaları sayabilmek için, ufak yuvarlak çakıl taşlarına sahip olması, veya kesilmiş bir ağaç dalı (sopa) üzerine çentik yapması icap edecekti. Bir taş veya sopa Üzerinde işaretlenmiş bir adet çentik, tek koyunu ifade ederdi. Belli bir zaman sonra, eğer her bir taş veya çentik için bir koyun yoksa, o insan bir veya birkaç koyunun kayıp olduğunu anlardı. Bu devrin insanları; sayıları bir yere kaydedip saklanmasını da biliyorlardı.
İlkçağ insanları, sayılar için kil tabletler üzerine çizikler kazmayı, veya kesilmiş ağaç dalına çentikler yapmaya başlamakla, ilk defa, sayıları yazılı olarak ifade etmiş oluyorlardı. İlkçağ insanının kullandığı bu işaretler, rakam ve sayıların ilk yazılı ifadeleridir.
Bunların yanında; ilkel insanlar, sayıları belirtmek için, değişik ses ve kelimeler de kullanmışlardır. Bugün sayıları belirten standart hale gelmiş sembol (şekil) ve sözcükler vardır. Günümüzde; sayılar, hem 1, 2, 3, … gibi sembollerle ve hem de; bir, iki, üç, … gibi kelimelerle ifade edilmektedir. Bugün dört adet kalemi, “dört kalem” kelimesi ile belirtip “4″ sembolü ile gösterebiliyoruz.
Bilinen en eski sayma sistemlerinden biri, Eski Mısırlılara ait olanıdır. Eski Mısırlıların kullandıkları resim yazısının (hiyeroglif) başlangıç tarihi, M.Ö. 3300 yılına kadar geri gider. Eski Mısırlılara ait sayma sistemi, ilkçağ mağara, insanının önceleri kullandığı sayma sisteminin gelişmiş şeklidir.
Eski Mısır aritmetiği hakkındaki bilgilerimiz, papirüs tomarlarından elde edilmektedir. Bugün bu papirüsler; bilim tarihinde, M.Ö. 1900-1800 yılları için adlandırılan, Kahun ve Berlin papirüsleri ile, M.Ö. 1700 ile 1600 yılları için adlandırılan Hiksoslar Devrinden M.Ö. 1788-1580 kalma Rhind ve Moskova matematik papirüsleridir. Mısır matematiği hakkındaki diğer kaynaklar, birkaç parşömen tomarı ile kil ve tahta tabletlere dayanmaktadır.
Eski Mısır’da rakam ve sayılar bazı sembollerin (şekillerin) yan yana gelmesiyle ortaya çıkıyordu. Bütün rakamlar, 7 değişik şeklin bir araya gelmesiyle ve yazım biçimi de, sağdan sola doğru ifade ediliyordu
Bugün Kullanılan sembollerle ifade

Sayıları da, bu sembollerle göstererek bir sayı sistemi geliştirmişlerdir. Eski Mısırlıların, 1 den 1.000.000 a kadar olan sayıları göstermek ve yazmak için kullandıkları semboller (şekiller) yukarıda gösterilmiştir.
Tablonun incelenmesinden anlaşılacağı gibi, 9 sayısını ifade etmek için, 9 ayrı şekil, 90 sayısını ifade edebilmek için, 9 adet başka bir şekil; 99 için 18 aynı şekil, 999 sayısı için ise, 27 ayrı şekil (sembol) kullanmak gerekli olmaktadır.
Eski Mısırlılar; bu sembolleri, gerektiğinde tahta, ağaç ve taş üzerine de oymuşlardır. Bu rakamları bir kaç kez kullanarak, istenilen sayıları göstermişlerdir. Bu sistemde; gruplamalar onarlık yapıldığından, sistem onluk sistemdir.
Eski Mısır sistemi, aşağıdaki belirtilen özelliklerinden dolayı, mağara insanının kullandığı sistemin geliştirilmiş şekli idi:
a) Bir kümede bulunan şeylerin toplam sayısı, sadece bir tek sembolle belirtilmiştir. Örneğin: 10 sayısının bir topuk kemiği sembolü ile belirtilmesi gibi.
b) Diğer sayıları göstermek için, aynı semboller tekrarlanmıştır.
c) Bu sistemde 10 luk gruplar esas alınmıştır. On düşey çizgi, bir topuk kemiği sembolünü, on topuk kemiği sembolü de, bir çengel sembolüne eş değerdir. Bu şekilde devam eder. Konu hakkında bir fikir vermesi bakımından aşağıdaki tabloda on tabanlı sayıların, eski Mısır sayma düzeninde nasıl yapıldığı gösterilmiştir.Eski Mısırlılar sıfır kavramını da bilmiyorlardı ve sıfırı gösterecek bir işaret (sembol) kullanmamışlardı. Fakat sayıları, çarpma ve çıkarma tablolarına, ehramların yapılış tarihlerinden itibaren sahip bulunuyorlardı.
Mezopotamyalılarda rakamlar, çivi yazısında görülen çivi yada oduncu kamasına benzeyen şekillerden ibarettir.
Bu işaretlerin (sembollerin) uygun biçimde, yan yana veya büyük sayıları gösterebilmek için toplu olarak veya tekrarlayarak grup halinde yazmak suretiyle 60′a kadar sayıları ifade edebiliyorlardı.
Bu tür yazım şeklinde, 0.1 ve 0.01 ile 0.001 gibi rakamların arasındaki farkı anlamak bir hayli güçtü. Bunu anlayabilmek için; metin, konu ve karine yardımıyla sonuç çıkarma yollarına gidilirdi.
Mezopotamyalılar da, sıfır sembolünü kullanmamışlardır. Ancak astronomilerinde bu maksatla, özel bir sembol kullandıkları anlaşılmaktadır.

Kaynaklar; çivi yazısından önceki resim yazısı (hiyeroglif) devresine tekabül eden safhada, en eski Mezopotamya rakamları olarak, aşağıdaki sembollerin kullanıldığını belirtir:Yukarda dikkat edilirse, 1 ve 10 sembollerinin temel olarak alındığı görülmektedir. Öteki 60, 600, 602, 603 gibi rakam sembolleri de, bu iki rakamın gelişmiş ve değişik biçimde gösterilmiş işaretlerden ibarettir. Bundan şu sonucu çıkarmak mümkün, 10 sembolünü düşünmezsek, altmış tabanlı (seksimal) bir sistem elde edilmektedir. Bu gelişimin tedrici bir şekilde yani yavaş yavaş yer almış olduğu da anlaşılmaktadır. Babil Sayma Sistemi
M.Ö. 2000 yıllarında Mezopotamya’da yaşayan Babillilerin, bilimin çoğu dalında, oldukça ileri bir seviyeye ulaşmış oldukları bilinmektedir. Öyle ki; Babil şehrini zamanın bilim merkezi haline getirmişlerdir. Özellikle matematik ve astronomide çok ilerlemişlerdir.Babilliler, 59′dan büyük sayıları da, basamak düşüncesinden yararlanarak yazdılar. 60 sayısını taban olarak kullandılar. Gruplamalarını 60′lık olarak, yani 60×2 = 120, … şeklinde yaptılar. Böylece ilk kez sayılarda basamak fikrini gösterdiler. Babiller, sayıları yazarken iki tane sembol ve bulunmayan basamaklar yerini doldurmak için de, (( : )) işaretini kullanmışlardır.
Babil rakamları arasýnda da, sıfır rakamını gösteren bir sembol yoktur. Rakamları sağdan sola doðru yazarak ifade ettikleri anlaşılmaktadır. Babilliler, kil tabletler üzerine “sitilüs” adı verilen tahta parçası ile yazarlardı. Bu tür yazıya çivi yazısı denir. Kağıt yapmayı, henüz bilmediklerinden, kilden yapılmış levhalar kullanmışlardır. Dört Temel İşlem
Toplama: Rakamları (işaretleri) yan yana yazarak yapıyorlardı.
Çarpma: Toplama işlemine benzer, çok yorucu bir yol uyguluyorlardı. Bu kadar uzun işlemlerin zorluğu karşısında, özel çarpma tabloları hazırlamışlardır.
Kesirler: Çoðu zaman kesirler, paydası birim (yani 60) olan sayı ile ifade ediliyordu. Yalnız, çok eski tarihten beri, Babil’de 1/3, 2/3, 5/6 gibi bir çok basit kesirlerin kullanıldığı da anlaşılmaktadır.
Romalılar, Eski Mısırlıların yıllarca önce yaptıkları gibi, önceleri, bazı sembolleri tekrarlayarak sayıları yazarlardı. (Bakınız Örnek l.) Sonraları da, çıkarmadan yararlanarak, daha kısa yazma yollarını ortaya koydular. (Bakınız: Örnek II.)
Örnek l :
XXXXX = 50
MDCLXVI = 1000 + 500 + 100 + 50 + 10 + 1 = 1666
DLXIII = 500 + 50 + 10 + 1 + 1 + 1 = 563Örnek II :
XC = 100 -10 = 90
IX = 10 -1 = 9
Başlangıçta değişik bazı sembol ve harfleri, rakam olarak kullanmışlardır. Bu rakamları, ilk olarak Romalılar kullandıkları için, aritmetikte “Roma Rakamları” ya da “Romen Rakamları” olarak adlandırılır.
Kaynaklar, Roma rakamlarının bir elin parmaklarından esinlenerek ortaya konduğunu belirtir. Romalılar, bugün kullandığımız l, 2, 3, 4 rakamları yerine I, II, III, IIII sembollerini ve 5′i belirtmek için de, V şeklinde bir el işaretini sembol olarak kullandılar. 10′u belirtmek için de V sembolünü, değişik biçimde iki kez kullanarak X sembolünü elde ettiler. (Çaprazlanmış iki düşey çizgi.) Diğer rakamları da alfabelerindeki harflerden aldılar.
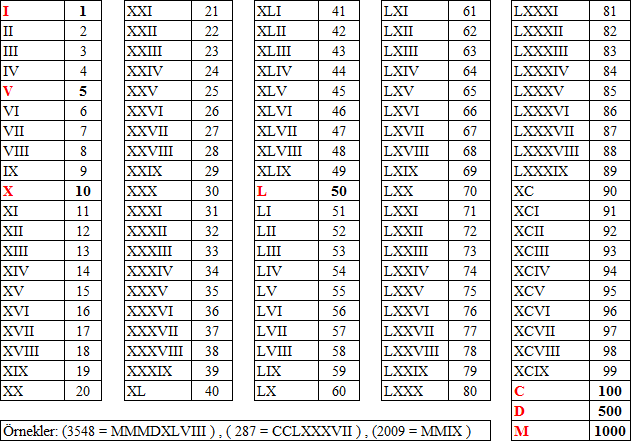
Romalılar sayıları belirtmek için, 7 ayrı harfi rakam olarak kullanmışlardır. Aşağıdaki tabloda, Roma rakamları gösterilmiştir.
Roma Sayma Düzeninde | I | V | X | L | C | D | M |
| Onluk Sayma Düzeninde | 1 | 5 | 10 | 50 | 100 | 500 | 1000 |
Roma rakamlarına dayalı, Roma sayma düzenine göre, toplama ve çıkarma işlemlerinin yapılmasında, bazı temel özellik ve sınırlamalar vardır. Bunları özetlersek :
A -Toplama İşlemindeki Özellik ve Sınırlamalar
a) Yanyana yazılan ve aynı sembolü gösteren, iki ya da üç temel rakam birbiriyle toplanarak, toplama karşı gelen sayı elde edilir .Örnek :I I I = 1 + 1 + 1 = 3
X X = 10 + 10 = 20Uyarı : Bu rakamların yazılışları ile ilgili önemli özellik : I, X, C sembolleri yanyana, 3′ten fazla; V, L, D, M sembolleri de, 1′den fazla yazılamaz.b) Büyük rakamların sağına yazılan küçük rakamlar, kendisi ile toplanarak toplama karşı gelen sayı elde edlir.Örnek :
XV = 10 + 5 = 15
DLXI = 500 + 50 + 10 + 1 = 561C) Küçük değerleri gösteren semboller (rakamlar), büyük değerleri gösteren sembollerin sağına yağıldığında, bu değerler toplanarak toplama karşı kelen sayı elde edilir.Örnek :
MDCLXVI = 1000 + 500 + 100 + 50 + 10 + 5 + 1 = 1666
DLXI = 500 + 50 + 10 + 1 = 561
XV = 10 + 5 = 15
DLXI = 500 + 50 + 10 + 1 = 561C) Küçük değerleri gösteren semboller (rakamlar), büyük değerleri gösteren sembollerin sağına yağıldığında, bu değerler toplanarak toplama karşı kelen sayı elde edilir.Örnek :
MDCLXVI = 1000 + 500 + 100 + 50 + 10 + 5 + 1 = 1666
DLXI = 500 + 50 + 10 + 1 = 561
B -Çıkarma İşleminde Özellik ve Sınırlamalar
a) 5 ile başlayan V, L, D sembolleri, çıkarma amacı ile, kendinden büyük değer belirten sembollerin soluna yazılmaz.b) Bir sayı, ancak aşağıdaki durumlarda çıkarılabilir.
I sadece V ve X den çıkarılabilir.
X sadece L ve C den çıkarılabilir.
C sadece D ve M den çıkarılabilir.
c) Küçük değerli semboller, büyük değerli sembollerin, soluna yazıldığında, büyük değerden küçüğü çıkarılır, bu fark sayıyı verirÖrnek :
IX = 10 -1 = 9
XL = 50 -10 = 40
d) İki büyük değerli sembol (rakam) arasına yazılan küçük değerli sembol, sağındakinden çıkarılmak suretiyle, sonuca denk gelen sayı elde edilir.Örnek :
CXL = 140
LIX = 59
d) Roma sembollerinin değer bir özelliği de, binleri göstermek için sembolün üzerine bir yatay çizgi, milyonları göstermek için de; ilgili sembolün üzerine iki yatay çizgi çizilerek ifade edilir.Örnek :
Görülüyor ki; Roma sayma düzeni, sadece toplama ve çıkarma işlemine dayanmaktadır. Sıfır ve basamak sistemi (kavramı) yoktur. Bu nedenle, aritmetik işlem yapmaya uygun değildir. Şöyle ki : Roma’da Forum Meydanı’ndaki süslü hitabet kürsüsünün “Columna Restrata” sütünunda 2.200.000 sayısını belirtmek için yirmi iki adet “yüz bin” i gösteren sembol (sayı işareti) oyulmuştur.
Roma rakamları bu özellikleri dolayısıyla; bugün matematik işlemleri yapmak amacıyla kullanılmamaktadır. Ancak, çok sınırlı olan, bazı özel gösterimler için kullanılmaktadır.
Tarih Öncesi Çağlarda Aritmetik
Sayı ve biçime ilişkin kavramlarla tanışmamız Yontma Taş Devri’ne kadar uzanır .Yüzbinlerce yıl boyunca insanlar , hayvanların yaşadığı koşullardan pek farklı olmayan bir biçimde mağaralarda yaşadılar .Enerjilerinin çoğunu nerede yiyecek bulurlarsa onu toplamaya harcıyorlardı .Avlanmak ve balık tutmak için silahları , birbirleriyle anlaşmak için konuşma dilini geliştirdiler .Yontma Taş Devri’nin sonlarına doğru da yaratıcı sanatlarla heykelcikler ve resimler yaparak yaşamlarını renklendirdiler .Fransa ve İspanya’daki yaklaşık 15.000 yıl öncesinin mağara duvar resimlerininayinsel bir anlamı olabilir , ama bunun ötesinde de üstün bir biçim anlayışı gösteriyorlardı .
Maden Devrinde ise bunun aksine ticaret öylesine gelişmişti ki , yüzlerce mil uzaklıktaki köyler arasındaki ilişkilerin izleri fark edilebiliyordu .Önce bakırın daha sonra da tuncun eritilmesiyle bu metallerden araçlar ve silahlar yapıldı .Bu da ticaretin ve yeni dillerin daha da gelişmesine yol açtı .Bu dillerdeki nesnelerin çoğunlukla somut ; yani elle tutulur ve gözle görülür nesneleri belirtmesine ve az sayıda olmasına karşın bazı sayısal terimler ortaya çıktı .Benim düşüncelerime göre matematiğin ilk kez ortaya çıktığı çağ Maden Çağıdır .
Ünlü bir matematikçi olan Adam Smith’in “insan aklının ürünü en soyut düşünceler” olarak tanımladığı sayısal terimlerin kullanılmaya başlanması çok yavaş oldu .Bunlar ilk ortaya çıktıklarında bir cismin sayısını değil niteliğini gösteriyordu .Örneğin ; “bir insan” değil sadece “insan” kavramını gösteriyordu .Sayısal kavramların bu niteliksel kökenlerinin izleri hala Yunanca ve Keltçe gibi bazı dillerdeki ikili terimlerde görülebilir .Sayı kavramı geliştikçe toplama yoluyla
daha büyük sayılar oluşturuldu :2 ile 1 toplanarak 3 , 2 ile 2 toplanarak 4 , 2 ile 3 toplanarak 5 bulundu .
İşte bazı Avustralya kabilelerinden örnek :
Murray Nehri : 1 =enea , 2 =petcheval , 3 =petcheval-enea , 4 =petcheval – petcheval
Kamilaraoi : 1 =ma , 2 =bulan , 3 =guliba , 4 =bulan bulan , 5 =bulan guliba , 6 =guliba guliba
Zanaatlerin ve ticaretin gelişmesi sayı kavramının netleşmesine yardım etti .Sayılar , ticaret yaparken doğal bir yöntem olan bir ya da iki elin parmakları kullanılarak daha büyük birimlerin içinde gösterildi .Buna örnek olarak şimdiki okullarda okuyan küçük sınıflarda ki çocukların sayma yöntemini verebilirim .Bu olayın sonucunda önce 5 sonra 10 tabanlı sayı sistemleri oluşturulup , bunlar toplama ve bazen çıkarma ile tamamlandı .Böylece 12, 10 + 2 olarak ya da 9 ,10-1 olarak algılandı .Bazen de taban olarak el ve ayak parmaklarının toplam sayısı olan 20 kullanıldı .Yapılan araştırmalara göre Amerikan yerlilerinin kullandığı 307 sayı siteminden 146’sı onluk , 106’sı onluk , onikilik ve yirmilik sayı sistemlerinin karışımıydı .Çoğu kişi tarafından yamyam olarak bilinen Amerikan yerlilerinin bu kadar çok sayı sisteminin olması önce bana biraz garip geldi .Fakat sonra , onların da en az bizim kadar zeki olduklarını anladım .Yirmili sayı sisteminin en tipik biçmi Meksika’da Mayalar ve Avrupa’da Keltler tarafından kullanıldı .
Sayılar kümelere ayrılarak , tahtanın üstüne çentik , ipin üstüne düğüm atılarak ya da deniz kabuklarının beşli yığınlar biçiminde düzenlenmesiyle sayısal kayıtlar tutuldu .Bu yöntemler eski zaman hancılarının çetele tutma yöntemlerine benziyordu .Böyle yöntemlerden 5 , 10 , 20 gibi özel simgelere geçilmesi çok kolay oldu .Benzer simgeler uygarlığın doğuşu da denen yazılı tarihin başlangıcından beri kullanılmıştır .
Yontama Taş Devri’ne kadar uzanan en eski çetele çubuğu 1937’de Vestonica’da bulunmuştur .Bu ; genç bir kurdun 7 inç uzunluğundaki ön kol kemiğiydi ve üzerinde ilk 25’i beşli gruplar halinde düzenlenmiş 55 çentik bulunmaktaydı .Dizinin sonunda , önceki çentiklerden iki kat uzun bir çentik vardı .Yeni dizinin başındaki çentik yine 2 kat uzundu ve bunu 30 çentikten oluşan bir dizi izliyordu .
Böylece , sık sık söylenen “eski zamanlarda sayma parmaklara dayalıydı .” görüşü geçerliliğini kaybetmiş oldu .Yazı olmamasına rağmen Yontma Taş Devrin’deki insanların çetele çubuklarını duymak ilginç gelebilir .Fakat gerçek .
Parmaklar kullanılarak sayı saymak yani 5’erli 10’arlı saymak ancak toplumsal gelişimin belirli bir aşamasında ortaya çıkar .Bu aşamadan sonra sayılar bir tabana göre ifade edildi ve bu da büyük sayıların ortaya çıkmasına yardım etti .Böylece ilkel bir aritmetik ortaya çıktı .14 bazen 10+4 , bazen de 15-1 olarak gösteriliyordu .20’nin 10+10 değil de 2´10 olarak gösterilmesiyle çarpma başladı .Bölme , 10’un “vücudun yarısı” olarak gösterilmesiyle başladı , ama kesirlerin bilinçli bir şekilde oluşturulması hala çok enderdi .Kuzey Amerika’da kabilelerin ancak birkaçında böyle kesirler biliniyordu , çoğu durumda bu ½’ydi .Bazen 1/3
ya da ¼’de kullanılıyordu .Bir başka ilginç durum çok büyük sayılara duyulan ilgidir .Bu belki de tümüyle insana ait bir tutku olan sürünün büyüklüğü ya da öldürülen düşmanların çokluğunu abartma isteğinin sonucudur .Bu eğilimin kalıntıları İncil’de ve diğer kutsal metinlerde de ortaya çıkar .
Tarih Öncesi Çağlarda Geometri
Cisimlerin uzunluklarını ve içindekileri ölçmek gerekince , genelde insan vücudunun bölümleri kullanılarak ; parmak , ayak , karış gibi basit ölçüler kullanıldı .Arşın , kulaç adları bize bu geleneği hatırlatır .Ev yaparken Hint köylüleri de , Orta Avrupa’da kutup evi yapanlar da yapıları düz çizgiler boyunca ve yere göre dik açıyla yapmak için kurallar geliştirdiler .Örneğin ; “Düz sözcüğü “germek” sözcüğü ile ilgilidir ve iple yapılan işlemleri gösterir .”Doğru” ve “Keten kumaş” sözcükleri , dokumacılık ile geometrinin başlangıcı arasındaki bağlantıyı gösterir .Dokumacılık ölçmeye ilişkin ilginin başlama yollarından biriydi .
Cilalı Taş Devri insanı geometrik desenlere büyük bir ilgi duyuyordu .Çömleklerin pişirilmesi ve boyanması , sazların örülmesi , sepet yapımı ve kumaş dokumacılığı , daha sonra da metallerin işlenmesi , düzlemsel ve alansal ilişkilerin kavranmasını geliştirdi .Dans figürleri de bunda rol oynamış olmalı ki Cilalıtaş Devri’nde yapılan süslemelerde benzerlik ve simetri görülür ; eş şekiller kullanılırdı .Bazı tarih öncesi desenler de üçgensel sayılar , bazılarında ise “kutsal” sayılar yer alıyordu .Pisagor matematiğinde önemli rol oynayan üçgensel sayıların oluşturulma çabaları yansımaktadır .
Bu tür desenler tarih boyunca yaygın olarak kullanılmıştır .Bunların çok güzel örneklerine Girit’teki Minos ve erken dönem Yunan vazolarında , daha sonra Bizans ve Arap moziklerinde , Pers ve Çin duvar halılarında rastlanır .Bu ilk desenlerin dinsel ya da büyüsel bir anlamı olabilir , ama zamanla görsel çekicilikleri ön plana çıkmıştır .
Taş Devri dinlerinde , doğa güçlerine egemen olma çabasının ilkel bir biçimini fark edebiliriz . Dinsel törenler büyü ile iç içeydi .Büyü öğesi de o zamanlar var olan sayı ve biçime ilişkin kavramlarda , heykel , müzik ve resimlerde içeriliyordu .3,4,7 gibi sihirli sayılar , Pentalpha ve Swastika gibi sihirli biçimler vardı .Matematiğin toplumsal kökenleri modern zamanlarda silikleşmişse de insanlık tarihinin ilk dönemlerinde bu kökler açıkça görülebilmektedir ve bazı yazarlar , matematiğin bu yönünün onun gelişiminde belirleyici olduğu görüşündedir .”Modern” sayı bilimi , Cilalı hatta belki de Yontma Taş Devri’nin büyü törenlerinin mirasıdır .
Zaman Kavramı
En ilkel kabilelerde bile bir “zaman” kavramına rastlanır ve bunun sonucu olarak da Güneş Ay ve yıldızların hareketleriyle ilgili bazı bilgileri edinmişlerdi .Bu bilgiler , çiftçilik ve ticaret geliştikçe daha bilimsel bir nitelik kazanmaya başladı .Bitkilerdeki değişimlerin Ay’daki değişimlerle ilişkilendirildiği Ay takviminin kullanılması , insanlık tarihinin çok erken dönemlerine kadar uzanır .İlkel insanlar gündönümünü ya da şafakta yedi yıldızlı Süreyya burcunun yükselişini ilgiyle izliyordu .İlk uygarlıkları kuran insanların astronomi bilgilerinin kökeni tarih öncesi dönemlerden gelen bilgilere dayanıyordu .İlk insanlar , takım yıldızlarından denizcilikte yararlandılar .Astronomiye ilişkin bu gözlemlerinin sonunda kürenin , dairenin ve açısal yönlerin özellikleri hakkında bilgi edinildi .
Matematiğin başlangıcına ilişkin bu birkaç örnek bir bilimin tarihsel gelişiminin , şimdi bu alandaki öğretimde geliştirdiğimiz aşamalarla çakışmayabileceğini göstermektedir .İnsanlarca bilinen en eski geometrik biçimler olan düğümlere ve desenlere ancak son yıllarda bilimsel bir ilgi gösterilmiştir .Öte yandan , grafikle gösterim ya da istatistik gibi matematiğin temel dallarının başlangıcı modern zamanlardadır .Bir matematikçi olan A. Speiser bu konuda şöyle düşünmektedir :
“Matematiğe girişin doğasında var olan sıkıcılığın ön plana çıkma eğiliminin geç başlangıcının sonucu olduğu söylenebilir ; çünkü yaratıcı bir matematikçi ilgi çekici ve güzel problemlerle uğraşmayı yeğler .”
ESKİ UYGARLIKLARIN MATEMATİKLERİ
Doğu Matematiği
Doğu matematiği uygulamalı bilim kökenliydi .Takvimin hesaplanması , tarımsal üretim ve bayındırlıkla ilgili işlerin örgütlenmesi , vergilerin toplanması uygulamalı aritmetik ve ölçme sorunlarına öncelikle ağırlık verilmesini gerektirdi .Bununla birlikte , yüzyıllar boyunca özel bir zanaat olarak gelişen bilim yalnızca uygulamaya yönelik değildi ; sırlar öğretilirken , soyutlamaya yönelik eğilimler de ortaya çıktı .Aritmetiğin cebire dönüşmesi yalnızca daha pratik hesaplamalar sağladığı için olmadı ; bu , aynı zamanda yazıcı okullarında öğretilen bir bilimin doğal bir gelişimiydi .Aynı nedenlerle ölçme ile ilgili bilgiler kuramsal geometrinin başlangıcını oluşturdu .
Mısır Matematiği
Mısır matematiğine ilişkin bilgilerimizin çoğu iki kaynağa dayanır .Bunlar 85 problemi içeren Rhind Papirüsü ve bundan belki de 200 yıl öncesine ait olan ve 25 problemi kapsayan Moscow Papürüsü’dür .Bu elyazmaları düzenlenirken , içerdikleri problemler zaten eskiden beri biliniyordu ; ama yakın dönemden , hatta Roma döneminden kalma az sayıdaki papirüsteki yöntemler de bundan farklı değildi .Kullandıkları matematik onlu sayı sistemine dayanıyordu ve 10’dan büyük her 10’lu birim için özel simgeler kullanılıyordu .Bu tür sistemleri Roma rakamlarından biliyoruz : MDCCCLXXVII = 1878 .Bu sistemi kullanan Mısırlılar , çarpmayı ardışık toplamalara indirgeyen , toplama ağırlıklı bir aritmetik geliştirdi .Örneğin , bir sayıyı 13 ile çarpmak için onu önce 4 ve 8’le çarpıyorlardı daha sonra çıkan sonucu sayının kendisine ekliyorlardı .Bu işlemi yaparak inceleyelim :
Normal çarpma işlemi :3´13=39
Mısırlıların kullandığı yöntem :
3´4 =12
3´8 =24
24+12 =36
36+3 =39
Görüldüğü gibi sonuç aynı .Mısır matematiğinin en önemli yönü kesirlerle yapılan hesaplamalardır .Bütün kesirler , payı bir olan birim kesirlerin toplamı olarak yazılırdı .
Bazı problemlerin teorik yanları ağır basıyordu .Örneğin 100 somun ekmeği 5 kişi arasında , her birine düşen pay aritmetik olarak artarak ve en büyük 3 payın toplamının yedide biri en küçük iki payın toplamına eşit olacak biçimde bölüştürülmesi problemi böyleydi .7 evin her birinin 7 kedisi , her kedinin kovaladığı 7 farenin olduğu problem , geometrik olarak artan bir serinin toplamının formülünü bildiklerini gösteriyordu .
Böyle problemler için yazılmış şiirler , şarkılar bile vardır .Şu şiiri anımsayalım :
“St. Ives’e giderken
7 karısı olan bir adamla karşılaştım
Her karısının yedi sepeti
Her sepetin yedi kedisi
Her kedinin yedi yavrusu vardı
Her yavrununda yedi çıngırağı vardı
Yavrular , kediler , sepetler , kadınlar ve çıngıraklar
Kaç tanesi St. Ives’e gidiyordu ?
Mezopotamya Matematiği
Mezopotamya matematiği , Mısır matematiğinin hiçbir dönemde ulaşamadığı bir düzeye erişti .Burada yüzyıllar içinde bile ilerlemeyi fark edebiliriz .M.Ö 2100’deki en eski metinlerde bile gelişmiş hesap izleri bulunur .Bu metinlerde 10’lu sistemin üzerine 60’lı sistemin eklendiği çarpım tabloları bulunmaktaydı .1 , 60 , 3600 ; hatta 60 üstü ve 60 üstü 2’yi gösteren çiviyazısı simgeler kullanılmıştı .Ama bu onların matematiğinin tipik özelliği değildi .Mısırlılar daha büyük her sayıyı yeni bir simge ile gösterirken , Sümerliler aynı simgeyi kullanıp değerini bulunduğu yere göre belirliyorlardı .
Ayrıca 60’lı sayı sistemi insanlığın kalıcı bir kazanımı oldu .Günümüzde kullandığımız saatin 60 dakika ve 3600 saniyeye bölünmesinin de , dairenin 360 dereceye , her derecenin 60 dakikaya , her dakikanın da 60 saniyeye bölünmesinin kökeni de Sümerliler’e kadar uzanır .Birim olarak 10 yerine 60’ın alınmasının sebebi ölçme sistemlerini birleştirmek olabileceği gibi 60’ın birçok böleninin olması da nedenlerden biri olabilir .
MISIR HİYEROGLİFLERİ
Eğer yazılarınızı eski Mısır hiyeroglifleriyle yazarsanız çoğu kişi bunları okumaya çalışmaktan vazgeçecektir .
Eski Mısır Hiyeroglifleri’nden Mısır rakamlarını öğrenmek çok kolaydır ; çünkü hepsinin bir görsel anlamı vardır .Büyük bir olasılıkla yazı yazmaya başlamadan once Mısırlılar , sayı saymak için parmaklarını kullanıyorlardı .Başka birinin okuması için sayı düzenlemeleri gerektiğinde de , yine büyük bir olasılıkla , yan yana sıralanmış yapraklar , ip parçaları ve çiçekler bırakıyorlardı .Neden mi böyle düşünüyoruz ? Çünkü daha sonradan hiyeroglif yazı sistemini geliştirdiklerinde , yaprak ip parçaları , çiçek ve hatta yılan ve iribaşlar kullanmışlar .
Hiç yorum yok:
Yorum Gönder